En esta entrada explicamos cómo determinar el amortiguamiento de la suspensión delantera de un automóvil. Para ello usamos los datos obtenidos en un ensayo realizado a un vehículo en un banco de suspensiones. Se ha excitado la rueda izquierda delantera llevándola hasta los quince hertzios mediante un motor con una leva excéntrica conectada a una placa. De modo que una vez que dejamos de excitar el automóvil con la placa tenemos asegurado el barrido de todas las frecuencias menores que quince hertzios.
El modelo de dos grados de libertad que hemos usado tiene un inconveniente: omite la barra estabilizadora. Para corregirlo sumamos la rigidez de la barra estabilizadora a la rigidez del resorte.
Veamos los parámetros del modelo de 2 g.d.l. usado en la siguiente figura:
Este modelo exige que recojamos tres lecturas de posición durante el experimento: la de la placa, la de la rueda y la de la carrocería.
Para ello empleamos sensores de posición (dos de ellos láser) y un ordenador portátil equipado con una tarjeta de adquisición de datos y con LabVIEW.
- Rigidez de los resortes: Kr = 20000 N/m.
- Rigidez de la barra estabilizadora: Ke = 9600 N/m.
- Rigidez K del modelo: K = Ke + Kr = 29600 N/m.
- Rigidez de los neumáticos: Kn =150000 N/m.
- Amortiguamiento del neumático: Rn = 300 Ns/m (despreciable).
- Peso del eje delantero sobre la rueda izquierda: Pi = 345 kg.
- Masa semisuspendida: mss = 30 kg (estimada).
- Masa M del modelo: M = Pi – mss = 315 kg.
Tratamiento de los datosHemos tomado datos con una frecuencia de muestreo de 2000 Hz durante 28 segundos. A continuación describimos algunos comandos de MATLAB utilizados.
Lectura de datos del fichero de texto:
arch=dlmread('ruedaizq10hz.txt');
L0=arch(:,1);
L1=arch(:,2);
Las señal del láser uno está retrasada 0.005 segundos respecto al láser cero. Por tanto lo corregimos de la siguiente forma:
L1=L1(10:56000,1);
L0=L0(1:55991,1);
Tenemos almacenada la información de cada láser en voltios. Usaremos las correspondientes rectas de regresión para pasar mm:
L0=(L0.*(-8.0376))-0.0884;
L1=(L1.*(-2.8638))-0.0121;
Aunque este apartado es muy dependiente del software y del hardware usado; puede servir de orientación a quien quiera realizar un experimento similar con otro equipo.
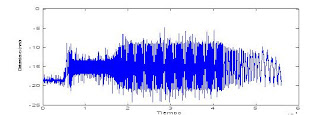
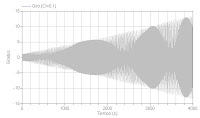
Gráficas obtenidasGraficando las lecturas del láser uno (x2) y del cero (x1) obtenemos:
Desechamos los transitorios y nos quedamos entre los 10 y los 20 s. En esas zonas calcularemos la frecuencia y la amplitud de x1 y de x2. Aplicando el zoom:
Amplitudes:
A1 = 5.7385 – 4.238 = 1.5005 mm
A2 = 7.9023 + 5.8214 = 13.7237 mm
Frecuencia (las dos señales tiene la misma):
Para disminuir el error hemos tomamos siete periodos.
Planteamiento y resolución de ecuacionesPlanteando el diagrama del sólido libre de la masa M obtenemos la siguiente ecuación diferencial:
Despreciamos el efecto del peso
Usando la transformada de Laplace:
Haciendo s=jw:
Tomando módulos:
Despejando nuestra incógnita (R):
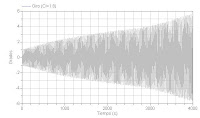
Validación de la hipótesis de masa semisuspendidaDeterminamos a partir de la señal de la placa su amplitud en el intervalo comprendido entre los 10 y los 20 s: Ao=12 mm.
Se han usado las siguientes sentencias MATLAB para obtener la gráfica:
arch=dlmread('ruedaizq10hz.txt');
p=arch(:,1);
p=arch(:,5);
p=p(10:56000,1);
p=(p.*(-18.2177))+49.5693;
plot (p)
Usando un procedimiento análogo al del apartado 5, obtenemos a partir de la siguiente ecuación el valor de la masa semisuspendida. Si el resultado es similar al supuesto (30 kg) la estimación será correcta.
De esta ecuación obtenemos dos valores:
m1 = 72.74 kg (la desechamos por estar fuera del intervalo de valores típicos)
m2 = 30.27 kg. Muy cercana a 30 kg => Hipótesis Correcta =>
R = 1854.098 Ns/m
Caracterización del comportamiento. A partir de las ecuaciones diferenciales que modelan el comportamiento de un determinado tipo de célula, hace una simulación intensiva y almacena su comportamiento en tablas.
